-
Posts
2898 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Store
Articles
Patch Notes
Everything posted by WanderingAries
-
The last ep surely left the opening for S2, but I'm not sure the series itself gave it enough momentum.
-

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
For the same reason that they apparently Intentionally reduced the lifespan of lightbulbs? -

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
Yeah, I'd wager that any prebuilt system, especially business devices, aren't designed to be upgradeable, thus allowing for the nose to the wall PSUs. -

[How2] Basic Installation Guide [Windows]
WanderingAries replied to WanderingAries's topic in Homecoming Launcher
I modified the related section to link the now existing FAQ post. I believe there wasn't a set link back when this was created as the app was still in beta status. -
And my brain went straight to... 😇🤡😹
-

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
Heh, I've never played wired for the most part and much of it is about convenience. I mean I Could run the wire across the hall again if I wanted to, but I'd rather avoid fall risks and the signal strength is good anyway. Even when CoX was in beta (I started around i2), I was converting to laptops. Now my TV is across the room from me as is the desktop PC, but my KB/M are wireless. IDK, if I were some hardcore FPSer, then I might care more. -

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
Heh, I've been using Dos since like v2, all of windows, MacOS since it was first given to schools, and one or two Linux flavors for beta testing (per request). Between that and the mobile device OSes, I'd say I'm pretty well rounded, experience wise. -

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
-

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
Repeat after me: "ALWAYS buy a PSU with 20%+ higher Wattage than what you need" And be careful when you upgrade/add parts. The Reason I have a 1kW PSU and GTX970 is because when I finally was able to afford the GTX770 I had the 750W PSU. They ran ok for a while and then suddenly something took them Both out. After checking, I had miscalculated somewhere in the build and that led to RMA time. -

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
What I find most amusing is where Apple likes to say "Macbook is best selling laptop" and yet their OS is only on a fraction of total devices. I wonder how many of what's in that graph is from Hackintoshes? 😛 -

Monterey post-installation issues
WanderingAries replied to WanderingAries's topic in Help & Support
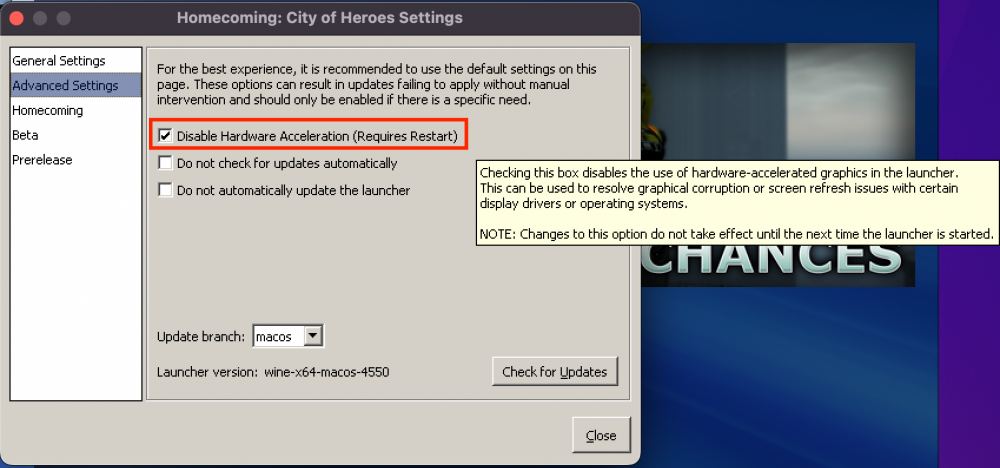
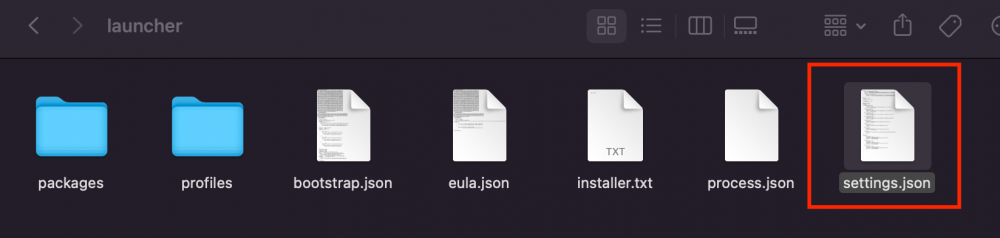
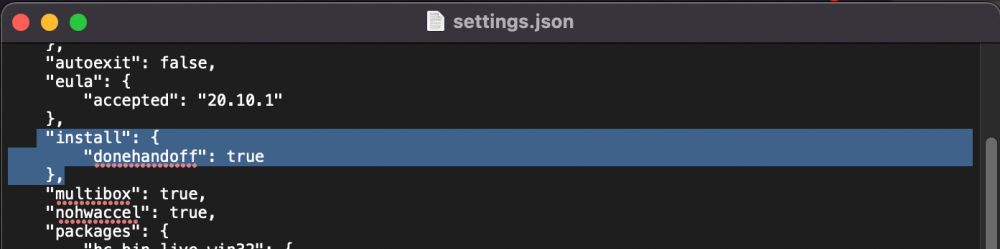
And I fixed that right up! Or at least figured out how to undo what I'd done. I had made a few tweaks in the settings like autoupdate, inactivefps, etc, but I'd also touched something related to Hardware Acceleration for some reason. IDK why I did, but that's what caused the error. So here's how to fix it when you do this exact thing. The thing I touched: (I had removed the check and not restarted the Mac yet) Open the folder shown: Open the File Indicated: Change the entry: (True means checked, False means unchecked) -

Monterey post-installation issues
WanderingAries replied to WanderingAries's topic in Help & Support
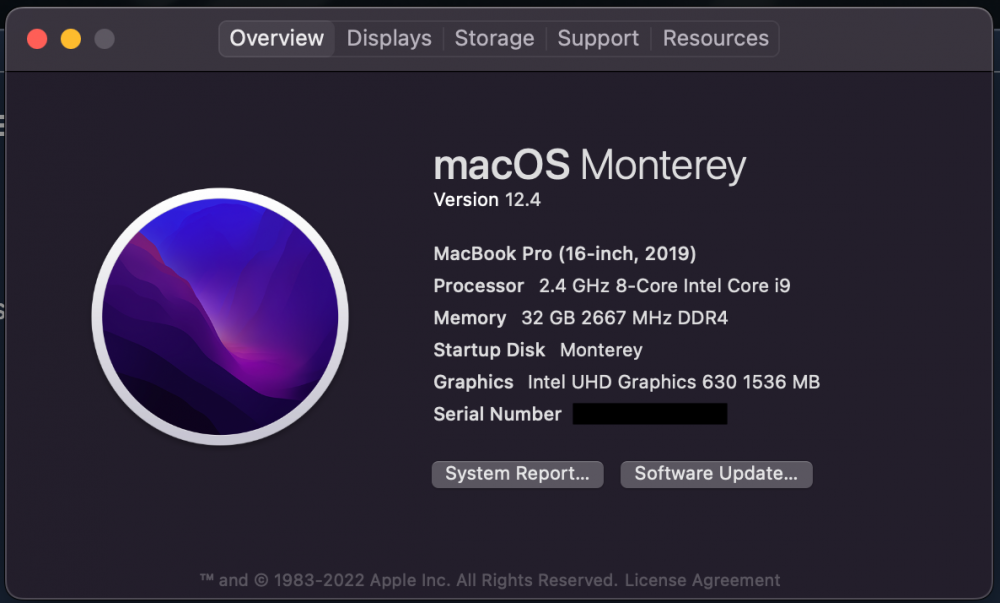
I'm running on this Mac: -
Because I'll be linking this eventually, here's the newest Mac that's prepping to take over the VM tooling around I do for fun. Mind you it's 6 generations newer than the 2012 (and the PC for that matter), but it's quite a bit lighter, quieter, faster, and the looks/sounds are nicer of course. I actually got the darker grey unit and I think I like that almost as much as the M1 Dark Blue color. Partially because of the fact that you can't upgrade anything, I've decided to not run bootcamp on here. I'll still tool around with Windows in VM, but I've generally got my PC for real use. It's taking a bit of getting used to the touchbar. Well, mostly trying Not to touch the back button when in the browser, but I find it is somewhat intuitive. The touchPad, however, is WAY too big for what I'm used to. I swear they meant for you to use both hands on it as it's causing me to have to move my hand more to the right because I use right click a lot.
-
So yeah, the more I looked into this, the more I realized that I'm liable to end up paying MORE to build the damned thing than I would to just grab a final gen intel Mac. Which is exactly what I did, but I blame PayPal as they gave me WAY too much credit on a whim and I paid a whole ~$50 interest to finance the thing for two years. The upside is that it's the newest computer in my personal possession, so if the older stuff fails, then I've got some time with this before it starts to show its age.
- 1 reply
-
- hackintosh
- mac mini
-
(and 3 more)
Tagged with:
-
I'll probably end up editing this a billion times as I'm in the middle of a thousand things at once, but here's what's happened so far with this "New to Me" Mac and Monterey. Note: For me, this is not even a priority, I'm just posting as whatever the solution is, it may help others. So basically, I installed the launcher/game just fine (very quick and easy), but it got weird when I loaded the game. On my first attempt, I got the login screen, but it absolutely would Not allow me to type. I could quite easily interact with it otherwise, but it would Not let me type. I poked at the on-screen settings and also noticed that the manual graphics slider didn't show the full range of screen dimensions (IE: It didn't show 1920x1080, etc). I could choose the native windowed/windowless, but the game wasn't seeing the 3k+ pixels this screen appears to have. Lastly, once I closed the game, that's the last time I could open it as I'm not only getting a crash handler page (see below). I've closed the launcher and tried again a few times, but same thing. I plan on reinstalling the game/launcher, but I've yet to see this popup before and it comes up prior to me even getting the login screen as before.
-

[How2] Basic Installation Guide [MacOS - Intel]
WanderingAries replied to WanderingAries's topic in Homecoming Launcher
Just updating a couple minor thing at the beginning as I've now tested it all the way through Monterey on raw hardware (plan on testing the beta OS just as soon as my onedrive downloads my VM fodder). I haven't launched the game yet (kinda downloading a ton of stuff to this newer Mac RN), but the launcher installed like a breeze. Everyone give a round of applause to @Manga for keeping this thing functional and optimizing it over time. Also, don't forget that donation link on the IR download page. 😉 -

Windows 11 and gaming performance
WanderingAries replied to Techwright's topic in General Discussion
Heh, I always find myself ahead of most these guys somehow. At least the ones in the front. Granted, anyone who actually reads up on hardware AND understands what it means should be able to give a real response. -
It is, but I wouldn't consider it a cake per say 😛
-
I was gonna say pie as many cakes are dry, but TBH, for Most pies I end up just carving out the innards and putting them in a bowl. 😛
-
This bugged the hell outta me because (while someone else has since stated that it Was there the whole time) I for the life of me only saw the one until the very end. I watched the whole sequence, listened to the dialog and in my head said "there's only one"...Until I saw the end and was like WTF?!?
-
I recently decided to get back into re-hackintoshing my i7 (on a dedicated SSD/BIOS config), but ran into a few compatibility snags. This made me sad for a few reasons ($$ for one) as I didn't realize that little things like RMAing my GPU for a newer one (way back) was enough to push me into a hole. And then there's Apple being Apple and dropping native support in OSes for older hardware. After thinking on it a bit, I started contemplating a completely new build, but with a more focused philosophy in mind. The only Real reason I 'want' one is to allow me to run Parallels / VMs for basic (possibly pointless) testing and to have a backup for when this 2012 MBP eventually fails. Originally, I went looking at deals on the latest Intel Macs, but damn these things still bite the budget even years later. Great for resale, bad for saving a buck. Now I think I've settled on what is essentially a Mac Mini, but in Hackintosh form. I've seen a few things online, but like many Hacks, the easy to find stuff isn't fully compatible to the point that I wouldn't get things like wifi OOB. So I posit you this question. Does anyone have a good lead on a relatively painless build for such a concept? I came across the Reddit thing, but I'm not a fan of the site as it feels more like Twitter / FB in that people will read your stuff for the first few days and after that nobody comes back. That or it just gets buried from the bulk of the masses, reducing your visibility. I've also been on places like TonyMac(?) for a long time now and it feels like things aren't any better TBH. IDK, if I had any sort of Real budget that allowed for just buying a Mac, then this'd be simpler, but I'll be lucky to be able to build what I'm imagining here without having to spread the cost over a long period of time.
- 1 reply
-
- hackintosh
- mac mini
-
(and 3 more)
Tagged with:
-

How to Use Paragon Chat Command /get_global_silent?
WanderingAries replied to BlackSpectre's topic in Help & Support